ΠΛΗΡΟΦΟΡΙΚΗ Γ’ ΓΥΜΝΑΣΙΟΥ
ΥΛΗ-ΘΕΜΑΤΑ ΓΙΑ ΤΙΣ ΓΡΑΠΤΕΣ ΕΞΕΤΑΣΕΙΣ
Κεφάλαιο 1: Εισαγωγή στην έννοια του αλγορίθμου
και του προγραμματισμού.
Σελίδες 176-185 (φωτοτυπίες)
Κεφάλαιο 2:Ο προγραμματισμός στην πράξη.
Σελίδες 186 – 201 (φωτοτυπίες)
Κεφάλαιο 1: Τα θέματα μπορεί να είναι:
- Θέματα ανάπτυξης
- Ερωτήσεις Σωστούς Λάθους
- Ερωτήσεις Πολλαπλών επιλογών
Πρέπει να γνωρίζετε καλά:
1.
Τι
είναι ο αλγόριθμος:
2.
Τι
είναι πρόγραμμα, προγραμματισμός, προγραμματιστής.
3.
Τι
είναι γλώσσα προγραμματισμού και ειδικότερα τι είναι γλώσσα μηχανής.
4.
Ποια
τα χαρακτηριστικά μιας γλώσσας προγραμματισμού (να τα αναφέρετε και να τα
περιγράφετε)
5.
Ποια
είναι τα κύρια εργαλεία ενός ολοκληρωμένου προγραμματιστικού περιβάλλοντος.
6.
Τι
ονομάζουμε συντακτικά και τι λογικά λάθη.
7.
Ποιες
οι κατηγορίες των προγραμμάτων μετάφρασης (μεταγλωτιστές, διερμηνείς) και ποιες
οι μεταξύ τους διαφορές.
8.
Ποια
τα στάδια για την εκτέλεση ενός αλγορίθμου από την Κ.Μ.Ε (σχήμα).
Κεφάλαιο 2:
Τα θέματα
θα είναι σαν τις ασκήσεις των φυλλαδίων:
Πρέπει να γνωρίζετε καλά:
·
τις
παρακάτω εντολές
|
Μπροστά
(μπ) |
Πίσω (πι) |
Δεξιά
(δε) |
Αριστερά
(αρ) |
Στυλόκάτω
(στκ) |
|
Στυλόάνω
(στα) |
Επανάλαβε |
Αν |
ΑνΔιαφορετικά |
Κάνε |
|
Δείξε |
Φράση |
Ερώτηση |
Ανακοίνωση |
ΤετραγωνικήΡίζα |
|
Δύναμη |
ΣβήσεΓραφικά |
|
|
|
·
Να
γράφετε και να καλείτε διαδικασίες με ή χωρίς παραμέτρους
Ενδεικτικά Θέματα. Τα θέματα που
ακολουθούν είναι ενδεικτικά. Δεν σημαίνει ότι θα είναι αυτά ακριβώς αλλά
παρόμοια.
1. Θα σας ζητηθεί να γράψετε τις εντολές που
δημιουργούν συγκεκριμένα σχήματα όπως για παράδειγμα:

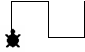
|
|
|
|
|
|
2. Θα σας
ζητηθεί να βρείτε ποια σχήματα παράγονται από συγκεκριμένες εντολές όπως για
παράδειγμα:
|
στκ δε 45 μπ 100 δε
90 μπ 100 αρ
90 μπ 100 δε
90 μπ 100 αρ
90 |
Α |
1 |
|
|
στκ δε 45 μπ 100 δε
90 μπ 100 μπ 100 αρ
90 μπ 100 |
Β |
2 |
|
|
Στκ δε 45 Μπ 100 δε
90 Μπ 100 δε
90 Μπ 100 δε
90 Μπ 100 |
Γ |
3 |
|
3. Διαδικασίες με την εντολή επανάλαβε: Θα
σας ζητηθεί να γράψετε διαδικασίες που θα δημιουργούν συγκεκριμένα σχήματα που
δημιουργούνται με επανάληψη όπως για παράδειγμα τρίγωνο, τετράγωνο, εξάγωνο,
κύκλος, ημικύκλιο ή αλλά σχήματα όπως για παράδειγμα:
4. Παραμετρικές Διαδικασίες: Θα σας
ζητηθεί να γράψετε διαδικασίες που θα δημιουργούν συγκεκριμένα γεωμετρικά
σχήματα που η πλευρά τους θα μεταβιβάζεται ως παράμετρος π.χ.
Για τρίγωνο
:πλευρά Για τετράγωνο
:πλευρά Για ορθογώνιο :ύψος
:πλάτος
5. Υπερδιαδικασίες: Θα σας ζητηθεί να
γράψετε διαδικασίες που θα δημιουργούν σχήματα καλώντας άλλες έτοιμες
διαδικασίες π.χ.
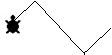
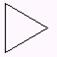
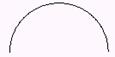
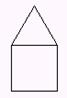
Εάν οι
διαδικασίες με ονόματα τετράγωνο, τρίγωνο και ημικύκλιο δημιουργούν τα σχήματα 1,2,3 (η χελώνα δείχνει την τελική
θέση) γράψτε νέες διαδικασίες με ονόματα σπίτι,
μύλος, λουλούδι που να σχεδιάζουν τα σχήματα 4,5,6 . Στις νέες διαδικασίες
μπορείτε να καλέσετε τις προηγούμενες:
|
|
|
|
|
|
|
|
6. Θα σας
ζητηθεί να υπολογίσετε τα αποτελέσματα εντολών δείξε π.χ.
|
Α/Α |
Εντολή |
Αποτέλεσμα |
|
1. |
Δείξε 20 /
4 |
|
|
2. |
Δείξε
δύναμη 5 2 |
|
|
3. |
Δείξε
ΤετραγωνικηΡιζα 36 |
|
|
4. |
Δείξε 10
* ( 6 – 4 ) /2 |
|
|
5. |
Δείξε [
(10 + 2) / 3 ] |
|
|
6. |
Δείξε “Καλημέρα |
|
7. Θα σας
ζητηθεί να δώσετε εντολές δείξε που εκτελούν συγκεκριμένες πράξεις όπως π.χ.
|
ΖΗΤΟΥΜΕΝΟ |
ΕΝΤΟΛΗ |
|
|
1. |
Προσθέστε
τους αριθμούς 234 32 728 |
|
|
2. |
Υπολογίστε
την δύναμη 123 |
|
|
3. |
Υπολογίστε
το μέσο όρο των αριθμών 10 15 3 |
|
|
4. |
Υπολογίστε
την παράσταση |
|
8. Θα σας ζητηθεί
να προβλέψετε τι θα εμφανίσουν αποσπάσματα κώδικα που περιέχουν μεταβλητές και
την εντολή κάνε π.χ.
|
για άσκηση1 κάνε "α 2 κάνε "β :α κάνε "β :β + :α δείξε (φρ :α :β) τέλος |
για άσκηση2 κάνε "χ 5 Κάνε "χ (:χ + 5) / 5 Κάνε "χ :χ * 4 δείξε :χ τέλος |
για άσκηση3 κάνε "κ 0 επανάλαβε 5 [κάνε "κ :κ + 1 δείξε :κ] τέλος |
9. Θα σας
ζητηθεί να γράψετε τις εντολές κάνε που πετυχαίνουν συγκεκριμένα αποτελέσματα
π.χ.
|
1. |
Δώστε σε
μία μεταβλητή χ την τιμή 5 |
|
|
2. |
Αυξήστε
την τιμή της μεταβλητής χ κατά 1 |
|
|
3. |
Τριπλασιάστε
την τιμή της μεταβλητής χ |
|
|
4. |
Κάντε την
τιμή της μεταβλητής χ το 1/5 της προηγούμενης τιμής |
|
|
5. |
Δώστε σε
μία μεταβλητή ψ την τιμή της μεταβλητής χ |
|
10. Θα σας ζητηθεί
να γράψετε διαδικασίες που λύνουν απλά υπολογιστικά προβλήματα π.χ.
Να διαδικασία η οποία θα «διαβάζει»
την βάση και το ύψος ενός τριγώνου και στη συνέχεια θα υπολογίζει και θα εμφανίζει
το εμβαδόν του. Ως γνωστό το εμβαδόν
υπολογίζεται από τον τύπο:
![]() όπου β η βάση και υ το ύψος του τριγώνου.
όπου β η βάση και υ το ύψος του τριγώνου.

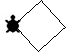


 2
2

 4
4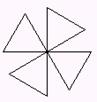 5
5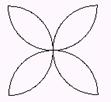 6
6